七（第5/6页）

我有感于上帝的记事本之厚重、造物主编织的蕾丝之精巧。即便你再如何拼命一眼一眼地摸索过去，只要出现短短一瞬间的疏忽，便会跟丢前进的线索。当你以为来到终点，因而欢呼雀跃之时，转瞬间便出现了更加复杂的纹样。

毫无疑问，博士肯定也曾抓到过好几段蕾丝边。那里在光下显现的又是怎样美妙的纹样呢？我祈愿博士的记忆里至今仍铭刻着那些美妙的纹样。

书中第三章的中间部分说明，费马大定理并非纯粹满足数学爱好者好奇心的一个谜，它与数论的根本是何等的密切相关。在这里，我找到了与博士所写的一模一样的算式。就在我漫无目的一页页往下翻的时候，这一行在我视野一角一闪而过，所幸我并没轻易放过它。我把便条和书进行了谨慎细致的比对。一点没错。它被称为欧拉公式。

名称是立刻知晓了，但要理解公式的含义还有困难。我站在书架之间，把与公式相关的书页翻来覆去阅读了好几遍。特别难懂的部分，就照博士所教的出声朗读了几遍。数学角仍旧只有我一个人，不用怕妨碍到任何人。我侧耳倾听着被吸进数学书的间隙里去的自己的声音。

π我懂，是圆周率。i博士也教过我，是－1的平方根，是虚数。麻烦的是e。e好像和π一样，也是无限不循环的无理数，是数学里最重要的常数之一。

首先必须从什么是对数入手。所谓对数，是指在求一个常数的多少次方幂时的指数值。此时，该常数称作“底”。例如，假设底为10，求100的对数（log10100）。因为100＝102，所以对数值为2。

在平常使用的十进制里，使用以10为底的对数比较方便，便将它取名为常用对数，不过从数学理论上讲，以e为底的对数似乎也担负着不可估量的职责，这一类称作自然对数。需要思考的是对数值，即e的多少次方幂能够得到已经给出的数字。也就是把e作为“自然对数的底数”。

至于关键的这个e，根据欧拉算出的结果，e＝2.71828182845904523536028……

小数点后面的数字无穷无尽。相比上述解释的复杂程度以及e的值，算式显得非常明快。

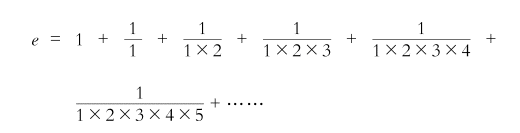
只不过，正因为明快，反倒使人感觉e这个谜越发的高深莫测了。

说到底，尽管取了个自然对数的名字，可究竟什么地方称得上自然了？不置换成符号便无法表达，无论多巨大的纸张也写不下，永远看不到最末尾，以这样的数字作底，难道不是不自然之极吗？

就像蚂蚁随意爬成的队伍，也像婴儿笨拙地堆起来的积木，这里罗列的数字看似纯属偶然、毫无秩序、不得要领，其实其中贯穿着合情合理的意志，因而更叫人束手无策。上帝的安排深不可测。而且必定有人能够察觉这种安排。尽管包括我在内的芸芸众生，并未公正地对他们所付出的辛劳表示过感谢。

我放下被书本的重量压麻痹的手，重新翻动书页，缅怀起十八世纪最伟大的数学家莱昂哈德·欧拉(4)。关于他，我一无所知，可仅仅将这一道公式拿在手里，便感觉仿佛感触到了他的体温。欧拉他运用一个不自然之极的概念，编写出了一道公式；他在貌似毫不相干的数字之间发现了自然的联系。

e的π乘i次方幂加1等于0。

我再一次看着博士的便条。两个数字，一个循环至尽头的尽头，一个绝不显露真面目、虚无缥缈，它们描画出简洁的轨迹，落于地上一点。虽然圆自始至终不露面，π却不期然地从空中飘落到e身边，来和生性腼腆的i握手。它们相互靠近，屏声静气地静静待着，直到一名人类进行了一次加法运算，令世界刹那间毫无征兆地风云变幻——一切重归0的怀抱。

欧拉公式是划破黑暗的一道流星，是漆黑的洞窟里刻着的一行诗。我一边赞叹其中蕴含着的美，一边把便条重新收进了月票夹。

走下图书馆的阶梯时，蓦然回首，数学角依旧空无一人、寂寂无声，依旧是谁也不知道那里隐藏着许多那般美好的事物。

第二天，我又去了图书馆，只为查阅另一桩之前一直记挂在心头的事情。我取出1975年地方报纸的缩印版，耐心地一页一页翻着厚厚一沓册子。在1975年9月24日的地区版上，果然刊登着我要找的报道。

23日下午4时10分左右，在××町3条丁目号国道上，××运输公司的××司机（28岁）驾驶的轻型卡车越出中间线驶入反向车道，与××大学数学研究所教授××先生（47岁）驾驶的自备车正面相撞。××先生脑部受到重创。坐在副驾驶座上该先生的大嫂××女士（55岁）右腿骨折，伤势严重。卡车司机也碰伤额头等处，但均为轻伤。警方认为事故原因在于昏睡驾驶，正在向肇事卡车司机调查案发经过……